1. If a dielectric is placed between two plates of a parallel plate capacitor, the value of capacitance:
- (A) increases
- (B) remains constant
- (C) decreases
- (D) none of these
CONCEPT:
Capacitance of a capacitor (C):
- The capacitance of a conductor is the ratio of charge (Q) to it by a rise in its potential (V), i.e.
C = Q/V
- The unit of capacitance is farad, (symbol F ).
Paralle Plate Capacitor:
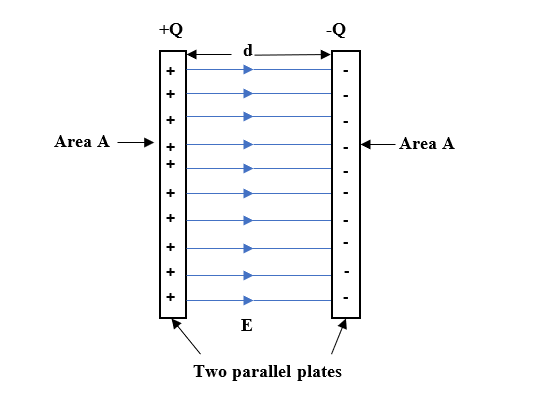
- A parallel plate capacitor consists of two large plane parallel conducting plates of area A and separated by a small distance d.
- The Mathematical expression for the capacitance of the parallel plate capacitor is given by
$C = \dfrac{ϵoA}{d}$
Where C = capacitance, A = area of the two plates, ε = dielectric constant (simplified!), d = separation between the plates.
EXPLANATION:
- When a dielectric slab of thickness t and dielectric constant K is inserted between the parallel plate capacitor, then the capacitance becomes
$ C = \dfrac{ϵoA}{d−t+ \dfrac{t}{K}} $
- From the above equation, it is clear that when a dielectric slab of thickness t is inserted then the effective distance between the parallel plate capacitor decreases, and hence capacitance increases. Therefore, option A is correct.
2. Charge on a capacitor of capacitance 1μf having potential difference 1 volt between it's plates will be:
- (A) Zero
- (B) 1 μC
- (C) 1 C
- (D) Infinity
CONCEPT:
We know that electric fields and voltage differences go hand-in-hand, and so it also turns out that the two plates are at different voltages. The size of this voltage difference ($V$) is related to the charges on the two plates ($Q$):
CALCULATION:
3. Force between two charge particles situated at a distance is F. If distance between the two charges is made half, then the value of electric force will be:
- (A) 4F
- (B) 2F
- (C) $\frac{1}{4}$F
- (D) $\frac{1}{2}$F
Explanation:
From Coloumb's law of electrostatic force we know,
$F = \dfrac{kq_1q_2}{r^2}$ (where, $k$ is a constant, $q_1$ and $q_2$ are two charges separated by distance $r$)
So, if the distance between the two charges is made half, with no changes of the charges, new distance becomes $\frac{r}{2}$
So, if now force acting between the same charges is $F$.
Then $F'= \dfrac{kq_1q_2}{(\dfrac{r}{2})^2} = 4\dfrac{kq_1q_2}{r^2} = 4 F$
So, that means, force will be 4 times of the initial value. Therefore, option A is correct.
4. Unit of $∈_0$ is
- (A) $\ce{\text{N.m}^{–1}}$
- (B) $\ce{\text{F.m}^{–1}}$
- (C) $\ce{\text{C.V}^{–1}}$
- (D) $\ce{\text{F.m}}$
| Epsilon Naught Units | Units |
|---|---|
| Epsilon Naught in SI | Farad per meter or $\text{F.m}^{-1}$ |
| Epsilon Naught in CGS | Columb square per Newton meter squared or $\dfrac{C^2}{\ce{N.m^2}}$ |
Therefore, option B is correct.
5. Two capacitors each of capacity C are connected in parallel. The equivalent capacity is:
- (A) 2C
- (B) C
- (C) $\frac{C}{2}$
- (D) $\frac{1}{2C}$
CONCEPT:
- The device that stores electrical energy in an electric field is called a capacitor.
- The capacity of a capacitor to store electric charge is called capacitance.
- When two or more capacitors are connected in such a way that their ends are connected at the same two points and have an equal potential difference for all capacitor is called the parallel combination of a capacitor.
- Equivalent capacitance (Ceq) for parallel combination:
Ceq = C1 + C2
CALCULATION:
Given, C1 = C2 = C
Here, C1 and C2 are connected in parallel, therefore the equivalent capacitance is
⇒ Cpara = C + C
⇒ Cpara = 2C
Hence equivalent capacitance = 2c and option A is correct.
NOTE:
- When two or more capacitors are connected end to end and have the same electric charge on each is called a series combination of the capacitor.
- Equivalent capacitance (Ceq) in series combination:
$\dfrac{1}{C_{eq}} = \dfrac{1}{C_1} + \dfrac{1}{C_2}$
Where C1 and C2 are two capacitors in the circuit.
6. Which of the following has unit $\dfrac{\text{volt}}{\text{metre}}$?
- (A) Electric flux
- (B) Electric potential
- (C) Electric capacity
- (D) Electric field
The electric field intensity is given as:
$E = \dfrac{−dx}{dV}$
Its unit is volt/metre. Therefore, option D is correct.
7. 1 amu is equal to:
- (A) 1.6 x $\ce{10^{–27}}$ kg
- (B) 1.6 x $\ce{10^{27}}$ kg
- (C) 1.6 x $\ce{10^{–31}}$ kg
- (D) 1.6 x $\ce{10^{–19}}$ kg
1 amu is equal to mass of proton which is equal to 1.67×10−27 Kg or 1.67×10−24 gm.
Therefore, option A is correct.
8. Dimension of charge is:
- (A) $\ce{AT}$
- (B) $\ce{AT^–^1}$
- (C) $\ce{A^–^1T}$
- (D) $\ce{AT^2}$
Current, $I =\dfrac{charge}{time}$
⇒ Charge, $q = I × t$
$[q] = [AT]$
Therefore, option A is correct.
9. Sum of charges on collecting plate and condensing plate of a charge capacitor is:
- (A) zero
- (B) 1 μC
- (C) 1 C
- (D) Infinite
Explanation:
Construction wise a capacitor is made up of two plates with some dielectric medium in between them. When there is a potential difference between the plates, then an electric field is developed and direction is dependant on the polarity of plates. One plate will be positive while the other is negative, so the sum of charges on collecting plate and the condensing plates will be zero.
10. If potential energy of an electric dipole of moment $\ce{\overset{->}{P}}$ in its position perpendicular to electric field $\ce{\overset{->}{E}}$ is taken zero, then its potential energy an angel θ with $\ce{\overset{->}{E}}$ and $\ce{\overset{->}{P}}$ is given by:
- (A) $\ce{\overset{->}{P}·\overset{->}{E}}$
- (B) –$\ce{\overset{->}{P}·\overset{->}{E}}$
- (C) $\ce{\overset{->}{P} x \overset{->}{E}}$
- (D) $\ce{PE (1-cos θ)}$
11. When a body is charged, its mass:
- (A) increases
- (B) decreases
- (C) remains same
- (D) may increase or decrease
12. Surface charge density of a conductor is σ, Electric field near it is:
- (A) $\ce{\frac{σ}{2∈_0}}$
- (B) $\ce{\frac{σ}{∈_0}}$
- (C) $\ce{\frac{2σ}{∈_0}}$
- (D) $\ce{\frac{σ}{3∈_0}}$
It depends upon whether the surface is a conductor or not. The electric field near some charge-carrying plate will be $\dfrac{\sigma }{2\epsilon_0}$, but if the point is near the surface of a conductor, then the electric field will be $\dfrac{\sigma }{\epsilon_0}$.
13. The electric field at a point near an infinite thin sheet of charged conductor:
- (A) $\ce{∈_0 σ}$
- (B) $\frac{σ}{∈_0}$
- (C) $\frac{σ}{2 ∈_0}$
- (D) $\frac{1}{2}σ∈_0$
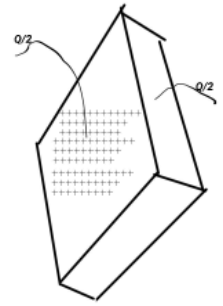
Let us understand first what is difference between a sheet and a plate in electrostatic.
Sheet => both side charge
Plate => one side charge
Here mentioned sheet, then surely charge will appear on both sides of the conductor.
Now, using the Gauss concept for finding an electric field.
Let $Q$ present in charged sheet conductor.
Because I clarify that both side charges are present in the sheet.
So, each side charge share = $\dfrac{Q}{2}$
Now, Gauss formula,
$Φ = \dfrac{Q_{net}}{2ε₀}$
Here, Qnet at one side = $\dfrac{Q}{2}$
Also, we know, $Φ$ { electric flux near the surface of sheet } = $E$ { electric field near the surface } × $A$ { cross-section Area of gaussian surface is chosen by us }
So, $EA = \dfrac{Q}{2ε₀}$
$E = \dfrac{Q}{2Aε₀} = \dfrac{Q/A}{2ε₀}$
We know, $Q/A$ = surface charge density = $σ$
$E = \dfrac{σ}{2ε₀}$
Hence, the electric field at a point near an infinite sheet of charged conductor is $\dfrac{σ}{2ε₀}$. Therefore option 3 is correct.
14. The electric potential due to a electric dipole at a large distance r from the center of the dipole is proportional to:
- (A) r
- (B) $\frac{1}{r}$
- (C) $\frac{1}{r^2}$
- (D) $\frac{1}{r^3}$
15. Two capacitors $\ce{C_1 = 2μF}$ and $\ce{C2 = 4μF}$ are connected in series and a potential difference (p.d.) of 1200 V is applied across it. It potential difference across 2 μF will be:
- (A) 400 V
- (B) 600 V
- (C) 800 V
- (D) 900 V
16. Minimum number of capacitors of 2μF each required to obtain a capacitance of 5 μF will be:
- (A) 4
- (B) 3
- (C) 5
- (D) 6
17. In the uniform electric field exists along X-axis, then equipotential is along:
- (A) XY-plane
- (B) XZ-plane
- (C) YZ-plane
- (D) anywhere
EXPLANATION:
If the uniform electric field will exist along x-axis then the equipotential surface will exist parallel to the yz-plane i.e. the planes that are normal to the x-axis.
An equipotential surface is a surface that comprises same electric potential at every point. Besides, the electric field is always perpendicular to it.
Therefore option C is correct.
18. Coulombian force is:
- (A) Central force
- (B) Electric force
- (C) both 'A' and 'B'
- (D) None of these
EXPLANATION:
Coulomb force also called electrostatic force or Coulomb interaction, attraction or repulsion of particles or objects because of their electric charge.
The electric force is operative between charges down to distances of at least 10-16 metre, or approximately one-tenth ($\dfrac{1}{10}$) of the diameter of atomic nuclei.
Therefor option C is correct.
19. The Quantum of electric charge in e.s.u. is:
- (A) 4.78 x $\ce{10^–^1^0}$
- (B) 1.6 x $\ce{10^–^1^9}$
- (C) 2.99 x $\ce{10^9}$
- (D) –1.6 x $\ce{10^–^1^0}$
20. Which of the following ratios is constant for an isolated conductor?
- (A) $\ce{\frac{Total charge}{Potential}}$
- (B) $\ce{\frac{Charge added}{Potential difference}}$
- (C) $\ce{\frac{(Total charge)^2}{Potential}}$
- (D) None of these
EXPLANATION:
The total charge to the potential ratio is constant for an isolated conductor.
$\dfrac{total \,charge}{potential} = isolated$
Therefore option A is correct.
21. 1 coulomb charge = .......... e.s.u.
- (A) 3 x $\ce{10^9}$
- (B) 9 x $\ce{10^9}$
- (C) 8.85x $\ce{10^–^1^2}$
- (D) None of these
22. The intensity of electric field at any point on the surface of a charged conductor is:
- (A) zero
- (B) perpendicular to the surface
- (C) tangetial to the surface
- (D) at 45° to the surface
23. The electric dipole moment of an electric dipole made up two opposite charges having $\ce{+ 3.2 x 10^–^1^9}$ C and $\ce{–3.2 x 10^–^1^9}$ separated by a distance $\ce{2.4 x 10^–^1^0}$m is:
- (A) 7.68 x $\ce{10^–^2^7}$ c-m
- (B) 7.68 x $\ce{10^–^2^9}$ c-m
- (C) 7.86 x $\ce{10^–^2^9}$ c-m
- (D) 7.86 x $\ce{10^–^2^7}$ c-m
24. The diamensional formula for $\ce{\ce{\frac{1}{2}∈_0 E^2}}$ is identical to that of:
- (A) $\frac{B^2}{2μ_0}$
- (B) $\ce{\frac{1}{2}B^2μ_0}$
- (C) $\frac{μ^{2}_0}{2B}$
- (D) $\frac{1}{2}Bμ^{2}_0$
25. In a region of constant potential:
- (A) the electric field is uniform
- (B) the electric field is zero
- (C) there can be no charge inside the region
- (D) both 'B' and 'C' are correct
26. Van de Graaff generator is used to:
- (A) store electric energy
- (B) builts up high voltage of few million volts
- (C) decelerate charge particle like electrons
- (D) both 'A' and 'B' are correct
EXPLANATION:
Van de Graff generator is an electrostatic generator which is devised to produce very high voltage by means of an endless belt collecting electrostatic charge from a source and transferring it to a large isolated metal sphere on which a large change accumulates.
Therefore, option B is correct.
27. One metallic sphere A is given positive charge whereas another identical metallic sphere B of exactly same mass as A is given an equal amount of negative charge, then:
- (A) Masses of spheres A and B still remains equal
- (B) Mass of A increases
- (C) Mass of B decreases
- (D) Mass of B increases
28. If +q charge is placed inside any spherical surface then total flux coming out from whole surface will be:
- (A) $\ce{q x ∈_0}$
- (B) $\frac{q}{∈_0}$
- (C) $\frac{∈_0}{q}$
- (D) $\frac{q^2}{∈_0}$
29. The electric potential in equatorial position of an electric dipole is:
- (A) $\ce{\frac{1}{4π ∈_0}\frac{p cos θ}{r^2}}$
- (B) $\ce{\frac{1}{4π ∈_0}\frac{p}{r^2}}$
- (C) $\ce{\frac{1}{4π ∈_0}\frac{p}{r}}$
- (D) Zero
30. Minimum number of capacitors each of 8 μF and 250 V used to make a composite capacitor of 16 μF and 1000 V are:
- (A) 8
- (B) 32
- (C) 16
- (D) 24
31. Metallic sphere of radius R is charged to potential V. Then charge q is proportional to:
- (A) V
- (B) R
- (C) both 'A' and 'B'
- (D) none of these
32. Dielectric constant for a metal is:
- (A) zero
- (B) infinite
- (C) 1
- (D) 10
33. A parallel plate condenser with a dielectric constant k between the plates has a capacity c and is charged to a potential V volt. The dielectric slab in slowly removed from between the plate and then reinserted. The network done by the system in this process is:
- (A) zero
- (B) $\ce{\frac{1}{2}(k – 1) cv^2}$
- (C) $\ce{\frac{cv^2(k – 1)}{k}}$
- (D) $\ce{(k – 1) cv^2}$
34. Energy stored in a capacitor and dissipated during charging a capacitor bear a ration:
- (A) 1 : 1
- (B) 1 : 2
- (C) 2 : 1
- (D) 1 : 3
35. A metallic sphere of radius 18 CM has been given a charge of $\ce{5 x 10^–^6 C}$. The energy of the charged conductor is:
- (A) 0.2 J
- (B) 0.6 J
- (C) 1.2 J
- (D) 2.4 J
36. When air is replaced by a dielectric medium of constant k, the maximum force of attraction between two chaarges separated by a distance:
- (A) increases k times
- (B) remains unchanged
- (C) decreases k times
- (D) increases $\ce{k^–^1}$ times
37. A parallel plate capacitor is made by placing n equally spaced plates connected alternatively. If the capacitance between any two adjacent plates is c then the resultant capacitance is:
- (A) nc
- (B) $\ce{\frac{c}{n}}$
- (C) (n + 1) c
- (D) (n – 1) c
38. Who established the fact of animal electricity?
- (A) Van de Graaff
- (B) Count Alessandro Volta
- (C) Gustav Robert kirchhoff
- (D) Hans christian oersted
39. Which one of the following is the unit of electric field?
- (A) Coulomb
- (B) Newton
- (C) Volt
- (D) N/C
- The SI unit of the electric field is Newtons per Coulomb (N/C).
- The SI unit of capacitance is Farad.
- The SI unit of pressure is Pascal.
- The SI unit of an electric current is Ampere.
- The SI unit of electric field strength is newtons per coulomb (N/C) or volts per meter (V/m).
Therefore, option D is correct.
40. If an electric dipole is kept in a uniform electric field then resultant electric force on it, is:
- (A) always zero
- (B) never zero
- (C) depend upon capacity of dipole
- (D) None
41. The number of electron taken out from a body to produce 1 coulomb of charge will be:
- (A) 6.25 x $\ce{10^1^8}$
- (B) 6.25 x $\ce{10^8}$
- (C) 6.023 x $\ce{10^2^3}$
- (D) None
42. Four equal charges q each are placed at four corners of a square of side a each. Work done in carrying a charge -q from its centre to infinity is:
- (A) zero
- (B) $\frac{\sqrt{2}q^2}{\pi\varepsilon_0a}$
- (C) $\frac{\sqrt{2}q}{\pi\varepsilon_0a}$
- (D) $\ce{q^2}{\pi\varepsilon_0a}$
43. The work done in rotating an electric dipole in an electric field:
- (A) W = PE (1 – cos θ)
- (B) W = PE tan θ
- (C) W = PE sec θ
- (D) None
44. If sphere of bad conductor is given charge then it is distributed on:
- (A) surface
- (B) inside the surface
- (C) only inside the surface
- (D) None
45. S.I. unit of permitivity is:
- (A) $\ce{C^2N^–^1m^–^2}$
- (B) $\ce{Nm^2C^–^2}$
- (C) $\ce{NC^–^2m^–^2}$
- (D) $\ce{N^–^1C^–^1m^–^2}$
46. Electric field in a cavity of metal:
- (A) depends upon the surrounding
- (B) depends upon the size of cavity
- (C) is always zero
- (D) is not necessarily zero
47. The dielectric constant of a metal is:
- (A) 0
- (B) 1
- (C) ∞
- (D) –1
EXPLANATION:
Metal is good conductor. So its $K=∞.$
Metal being a good conductor will easily allow charges to conduct and hence the permittivity will increase and its dielectric constant will tend to infinity.
Therefore, option C is correct.
48. The value of relative permittivity ($∈_r$) in air is:
- (A) zero
- (B) infinity
- (C) 1
- (D) 9 x $\ce{10^9}$
EXPLANATION:
The relative permittivity of a material is ratio of its (absolute) permittivity to the permittivity of vacuum. For air it is almost 1.
Therefore, option C is correct.
49. 1 coulomb is equal to in e.s.u.:
- (A) 3 x $\ce{10^9}$ e.s.u.
- (B) $\frac{1}{3}$ x $\ce{10^9}$ e.s.u.
- (C) 3 x $\ce{10^1^0}$ e.s.u.
- (D) $\frac{1}{3}$ x $\ce{10^1^0}$ e.s.u.
CONCEPT:
- Electric charge (Q): The property of matter which is responsible for electrostatic force is called an electric charge.
- The SI unit of charge is coulomb (C).
- The CGS unit if the electric charge is stat coulomb or esu (electrostatic system of units).
The relation between coulomb and stat coulomb is given by:
1 C = 3 × 109 stat Coulomb = 3 × 109 esu
EXPLANATION:
1 coulomb equals to 3 x 109 esu. Therefore, option A is correct.
50. The value of force acting on a charge particle in electric field is:
- (A) $\ce{qE}$
- (B) $\frac{q}{E}$
- (C) $\frac{E}{q}$
- (D) ${\sqrt{qE}}$
51. The dimensional representation of permittivity of free space ($\varepsilon_0$) will be:
- (A) $\ce{[MLT^4 A^2]}$
- (B) $\ce{[M^–^1 L^–^3 T^4 A^2]}$
- (C) $\ce{[ML^–^2 T^2 A^–^2]}$
- (D) None of these
52. When placed in a uniform field, a dipole experiences:
- (A) a net force but no torque
- (B) a torque but no force
- (C) both a net force and torque
- (D) neither a net force nor a torgue
53. A parrot comes and sits on a bare high power line. It will:
- (A) experience a mild shock.
- (B) experience a strong shock.
- (C) get killed instantaneously.
- (D) not be affected partically
EXPLANATION:
A parrot will not be affected practically because both legs are at the same potential. Thus, current cannot flow through its body.
Therefore, option D is correct.
54. The SI units of electric dipole moment are:
- (A) $\ce{C}$
- (B) $\ce{Cm^–^1}$
- (C) $\ce{Cm}$
- (D) $\ce{Nm^–^1}$
55. The unit of permittivity of free space (${\varepsilon_0}$) is:
- (A) $\ce{Coulomb^2/Newton-metre^2}$
- (B) $\ce{Coulomb^2/(Newton-metre)^2}$
- (C) $\ce{Coulomb/Newton-metre}$
- (D) $\ce{Newton-metre^2/$\ce{Coulomb}$
56. S.I. unit of electric flux is:
- (A) ohm. metre
- (B) ampere.metre
- (C) volt-metre
- (D) $\ce{(volt) (metre)^–^1}$
57. Two point charges of + 10 μc and –10μC are placed at a distance 40 cm in air. Potential energy of the system will be:
- (A) 2.25 J
- (B) 2.35 J
- (C) –2.25 J
- (D) –2.35 J
EXPLANATION:
Consider two charges: $q_1$ and $q_2$.
Charge on $q_1 = 10 \,×\, 10^{-6} \,C$.
Charge on $q_2 = -10 \,×\, 10^{-6} \,C$.
distance between them,
$r = 40 \,cm = -0.4 \,m$.
Now, electric potential energy between the charges is given as:
$U_E = \dfrac{kq_1q_2}{r}$ [$k$ = constant ($9 × 10^9 \,Nm^2/C^2$)]
$U_E = \dfrac{ -9 × 10^9 \,×\, 10 × 10^{-6} \,×\, 10 × 10^{-6}}{0.4}$
$U_E = \dfrac{-9}{4} × 10^9 × 10^{-9}$
$U_E = -2.25 \,J$
Thus, potential energy is given as $-2.25 \,J$. Therefore, option C is correct.
58. The stored energy, of a capacitor charged to 100 V is 1 J. Capacitance of the capacitor is
- (A) 2 x $\ce{10^4}$ F
- (B) 2 x $\ce{10^–^4}$ F
- (C) 2 x $\ce{10^2}$ F
- (D) 2 x $\ce{10^–^2}$ F
59. Which of the following values of n is not possible in relation Q = ne?
- (A) 4
- (B) 8
- (C) 4.2
- (D) 100
60. The relative permittivity $(∈_r)$ of a medium is:
- (A) $\frac{∈}{∈_0}$
- (B) $∈ × ∈_0$
- (C) $∈ + ∈_0$
- (D) $∈ – ∈_0$
61. Surface density of charge is equal to:
- (A) Total charge x Total area
- (B) $\ce{\frac{Total charge}{Total area}}$
- (C) $\ce{\frac{Total charge}{Total volume}}$
- (D) Total charge x Total volume
62. The unit of intensity of electric field is:
- (A) metre/volt
- (B) Joule/newton
- (C) Colomb/newton
- (D) Newton/coulomb
63. 1 V equals to:
- (A) 1 J
- (B) 1 $\ce{JC^–^1}$
- (C) 1 $\ce{CJ^–^1}$
- (D) 1 JC
64. The maximum amount of charge observed so far is:
- (A) 1 C
- (B) 4.8 x $\ce{10^–^1^3}$C
- (C) 1.6 x $\ce{10^–^1^9}$C
- (D) 1.6 x $\ce{10^1^9}$C
65. The ratio of electric force between two electrons to the gravitational force between them is of the order:
- (A) $\ce{10^4^2}$
- (B) $\ce{10^3^9}$
- (C) $\ce{10^3^6}$
- (D) 1
66. Charge on one proton in Coulomb is:
- (A) 1.6 x $\ce{10^–^1^9}$
- (B) 9.1 x $\ce{10^–^3^1}$
- (C) –1.6 x $\ce{10^–^1^9}$
- (D) None of these
67. The dielectric constant of water is:
- (A) 80
- (B) 60
- (C) 1
- (D) 42.5
68. The value of $\frac{1}{4π ∈_0}$ is:
- (A) 9 x $\ce{10^9 Nm^2c^–^2}$
- (B) 9 x $\ce{10^–^9 Nm^2c^–^2}$
- (C) 9 x $\ce{10^1^2 Nm^2c^–^2}$
- (D) 9 x $\ce{10^–^1^2 Nm^2c^–^2}$
69. SI unit of dielectric constant is:
- (A) $\ce{NM^–^2C^–^2}$
- (B) $\ce{NM^–^2C^2}$
- (C) No unit
- (D) F/N
OVERVIEW:
Dielectric constant of a medium is basically the relative permittivity, i.e. ratio of permittivity of the medium with respect to permittivity in free space. So, Its S.I. unit is farad per meter or $\ce{Fm^{-1}}$.
CONCEPT:
- Dielectric constant: The dielectric constant is a material of low electrical conductivity and has the ability to store electrical charge.
- It is defined as the ratio of the permittivity of the substance ϵ to the permittivity of the free space ϵ0.
Dielectric constant, $k = \dfrac{ϵ}{ϵ_0}$
EXPLANATION:
- As dielectric constant is the ratio of two like quantities i.e. permittivity, it has no units and dimensions.
Therefore, option C is correct i.e. no unit.
70. During lightning .......... charge is transferred to the earth:
- (A) positive
- (B) negative
- (C) both positive and negative
- (D) none
71. Which of the following relations is correct (for Electric Field Intensity)?
- (A) $\overset{→}{E} = \frac{\overset{→}{F}}{q}$
- (B) $\overset{→}{E} = q\overset{→}{F}$
- (C) $\overset{→}{E} = \frac{q}{\overset{→}{F}}$
- (D) $\overset{→}{E} = \frac{1}{4π ∈_0}\frac{q}{\overset{→}{F}}$
72. Electrostatic force is:
- (A) conservative
- (B) non-conservative
- (C) Both A and B
- (D) None of these
EXPLANATION:
The force is independent of the path. The force depends on the path. Gravitational Force, Spring Force, and Electrostatic force between two electric charges are examples of conservative force.
Q. Why electrostatic is conservative?
Solution: Electrostatic force is conservative because the work done by the force depends on the initial and the final points of a test charge.
Therefore, option A is correct.
73. $\ce{10^6}$ electrons are added to a pith ball. The negative charge on the pith ball is:
- (A) 1.6 x $\ce{10^–^1^3}$ C
- (B) 1.6 x $\ce{10^–^1^9}$ C
- (C) 1.6 x $\ce{10^–^2^5}$ C
- (D) None of these
74. When electrons are removed from an uncharged body, the body:
- (A) gets negatively charged
- (B) gets positively charged
- (C) gets negatively or positively charged depending upon its size
- (D) remains uncharged
EXPLANATION:
The electrons and protons are balanced in body.
If electrons are removed from body then positive charge is more than negative.
Thus, body will be positive charged.
Therefore, option B is correct.
75. When the velocity of a relativistic charged particle increases, it's specific charge:
- (A) decreases
- (B) increases
- (C) remains same
- (D) first decreases then increases
76. Which of the following is blocked by a capacitor?
- (A) A.C.
- (B) D.C.
- (C) Both A.C. and D.C.
- (D) Neither A.C. nor D.C.
77. The capacitance of a capacitor will decrease if we introduce a slab of:
- (A) copper
- (B) aluminium
- (C) zinc
- (D) None of these
EXPLANATION:
The capacitance of a capacitor will decrease with if we introduce a slab of copper. Aluminium and zinc are metals with very high dielectric constant. If a slab of a metal with high dielectric is introduced, the capacitance will increase.
Therefore, option A is correct.
78. $\ce{10^6}$ electrons are taken out of a pith ball. The positive charge on the pith ball is:
- (A) 1.6 x $\ce{10^–^1^3}$ C
- (B) 1.6 x $\ce{10^–^1^9}$ C
- (C) 1.6 x $\ce{10^–^2^5}$ C
- (D) None of these
79. In which of the following forms the energy is stored in the capacitor?
- (A) Charge
- (B) Potential
- (C) Capacitance
- (D) Electric field
80. The P.E. of an electric dipole is maximum when it makes an angle θ with electric field: The value of θ is:
- (A) $\frac{π}{2}$
- (B) $\ce{π}$
- (C) zero
- (D) $\frac{3π}{2}$
81. Choose the SI unit of electric potential energy:
- (A) Joule
- (B) Coulomb
- (C) Netwon per coulomb
- (D) Erg
82. Potential gradient is equal to:
- (A) $\frac{dx}{dV}$
- (B) $\ce{dx · dV}$
- (C) $\frac{dV}{dx}$
- (D) None of these
83. Which of the following is correct for the capacity of a parallel plate capacitor?
- (A) $\frac{∈_0 A}{d}$
- (B) $\frac{∈_0 d}{A}$
- (C) $\frac{d}{∈_0 A}$
- (D) $\frac{A}{∈_0 d}$
84. Choose the vector physical quantity:
- (A) Electric flux
- (B) Electric potential
- (C) Electric potential energy
- (D) Electric intensity
85. The surface density of charge is measure:
- (A) $\ce{Cm^–^1}$
- (B) $\ce{Cm^–^2}$
- (C) $\ce{Cm^–^3}$
- (D) $\ce{JC^–^1}$
86. What is the number of electrons in 100 g water?
- (A) 3.35 x $\ce{10^2^4}$
- (B) 3.35 x $\ce{10^2^5}$
- (C) 6.02 x $\ce{10^2^3}$
- (D) None of these
87. The electric potential of earth is taken as:
- (A) zero
- (B) infinity
- (C) unity
- (D) None of these
EXPLANATION:
Electric potential is defined as the potential difference between two points. So, electric potential at a point is defined with respect to a reference point. We take potential at the surface of earth as reference and is defined as zero.
By convection, electrostatic potential of earth is taken to be zero. It is considered that earth is a storehouse of infinite negative charges. So, ,most points are at a positive potential w.r.t it.
Therefore, option A is correct.
88. The value of electric potential at a distance r from a point charge q is:
- (A) $\ce{\frac{1}{4π ∈_0}\frac{q}{r}}$
- (B) $\ce{\frac{1}{4π ∈_0}\frac{q}{r^2}}$
- (C) $\ce{\frac{q · r}{4π ∈_0}}$
- (D) $\ce{\frac{1}{4π ∈_0}\frac{q^2}{r}}$
89. Electrical capacitance of earth of radius R is:
- (A) $\frac{R}{4π ∈_0}$
- (B) $\ce{4π∈_0R}$
- (C) $\frac{4π∈_0}{R}$
- (D) $\ce{4π∈_0·R^2}$
90. Electric-potential is equal to:
- (A) $\frac{q}{w}$
- (B) $\frac{w}{q}$
- (C) $\ce{wq}$
- (D) $\sqrt{wq}$
91. One farad is equal to:
- (A) 1 CV
- (B) 1 $\ce{CV^–^1}$
- (C) 1 $\ce{CV^–^2}$
- (D) 1 $\ce{CV^2}$
CONCEPT:
- Capacitor: A capacitor is a device that stores electrical energy in an electric field.
- It is a passive electronic component with two terminals.
- The effect of a capacitor is known as capacitance.
- Capacitance: The capacitance is the capacity of the capacitor to store charge in it. Two conductors are separated by an insinuator (dielectric) and when an electric field is applied, electrical energy is stored in it as a charge.
- The capacitance of a capacitor (C): The capacitance of a conductor is the ratio of charge (Q) to it by a rise in its potential (V), i.e.
-
$C = \dfrac{Q}{V}$
- The unit of capacitance is the farad, (symbol F ).
- Farad is a large unit so generally, we using μF.
EXPLANATION:
Units of capacitance:
- The SI unit of capacitance is the farad (F), named in the honor of Michael Faraday.
- The capacitance of conductor is 1 farad if the addition of a charge of 1 coulomb to it, increases its potential by 1 volt.
⇒$1 \,farad = \dfrac{1\,coloumb}{1\,volt}$
⇒$1F = \dfrac{1C}{1V}$
Therefore, option B is correct.
92. Potential energy of a charged conductor is:
- (A) $\ce{CV^2}$
- (B) $\ce{\frac{1}{2}CV^2}$
- (C) $\ce{\frac{1}{3}CV^2}$
- (D) $\ce{\frac{1}{4}CV^2}$
93. The potential gradient at which dielectric of the condenser just gets punctured, is known as:
- (A) dielectric constant
- (B) dielectric strength
- (C) dielectric resistance
- (D) dielectric number
94. The torque acting on electric dipole of dipole moment $\overset{→}{p}$ placed in electric field intensity $\overset{→}{E}$ is:
- (A) $\overset{→}{p}$ x $\overset{→}{E}$
- (B) $\overset{→}{p}$·$\overset{→}{E}$
- (C) $\ce{pE}$
- (D) $\overset{→}{p}$ / $\overset{→}{E}$
95. The lower of electric circiut is:
- (A) $\ce{V · R}$
- (B) $\ce{V^2 · R}$
- (C) $\ce{V^2/R}$
- (D) $\ce{V^2 · RI}$
96. S.I. unit of self-inductance is:
- (A) coulomb (C)
- (B) volt (V)
- (C) ohm (Ω)
- (D) Henry (H)
EXPLANATION:
Henry (symbol H) is the SI derived unit of self-inductance.
Therefore, option D is correct.
97. 64 identical drops each of capacity 5 μF combine to form a big drop. What the capacity of big drop?
- (A) 25 μF
- (B) 4 μF
- (C) 164 μF
- (D) 20 μF
98. Electrical permittivity of free space is equal to?
- (A) 9 x $\ce{10^9 Fm^{–1}}$
- (B) 1.6 x $\ce{10^{–9}C}$
- (C) 8.85 x $\ce{10^–^{12} Fm^{–1}}$
- (D) 8.85 x $\ce{10^{–9} Fm^{–1}}$
EXPLANATION:
Permittivity:
- Permittivity is a constant of proportionality that exists between electric displacement and electric field intensity
- It characterizes the tendency of the atomic charge in an insulating material to distort in the presence of an electric field
- The larger the tendency for charge distortion (also called electric polarization), the larger the value of the permittivity
- This constant is equal to approximately 8.85 × 10-12 farad per meter (F/m) in free space (a vacuum)
- In other materials, it can be much different, often substantially greater than the free-space value.
Therefore, option C is correct.
99. The electrical intensity inside a charged hollow sphere is
- (A) $\ce{E_0σ}$
- (B) $\frac{σ}{E_0}$
- (C) zero
- (D) $\frac{E_0}{2}$
EXPLANATION:
Shell theorem:
Intensity of electric field inside a uniformly charged hollow sphere is zero and outside the sphere we can assume the sphere to be a point charge present at centre and calculate E.
∴ The voltage is also constant inside hollow sphere as E = 0
Therefore, option C is correct.
100. Three capacitors each of capacity C are connected in series. The resultant capacity will be
- (A) $\ce{3C}$
- (B) $\frac{3}{C}$
- (C) $\frac{C}{3}$
- (D) $\frac{1}{3C}$
101. Two capacitors of capacity $C_1$ and $C_2$ are connected in parallel, then the equivalent capacity is:
- (A) $C_1 + C_2$
- (B) $\frac{C_1C_2}{C_1 + C_2}$
- (C) $\frac{C_1}{C_2}$
- (D) $\frac{C_2}{C_1}$
CALCULATION:
$C_1$, $C_2$ are connected in parallel then equivalent capacitance is calculated as
$V = V_1 = V_2$ ...(1)
$q = q_1 + q_2$
$∴ CV = C_1V_1 + C_2V_2$
From (1), $C= C_1 + C_2$
Therefore option A is correct.